OSE Piping Workbench Ports: Unterschied zwischen den Versionen
Ruslan (Diskussion | Beiträge) |
Ruslan (Diskussion | Beiträge) |
||
| (6 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 4: | Zeile 4: | ||
Every port is described by: | Every port is described by: | ||
| − | * Its position <math>a \in \mathbb{R}^3</math> | + | * Its position <math>a \in \mathbb{R}^3</math>. |
* A normal vector <math>n \in \mathbb{R}^3</math> which points out of the fitting and it is perpendicular to the port plane. | * A normal vector <math>n \in \mathbb{R}^3</math> which points out of the fitting and it is perpendicular to the port plane. | ||
* A 0 reference angle vector <math>r \in \mathbb{R}^3</math> it shows where is the degree 0°. <math>r</math> must lie in the port plane. | * A 0 reference angle vector <math>r \in \mathbb{R}^3</math> it shows where is the degree 0°. <math>r</math> must lie in the port plane. | ||
| + | All three vectors refer to local coordinates. | ||
| + | |||
| + | Instead of using three separate vectors, we represent the port by its position <math>A</math> and its orientation <math>A</math>. | ||
| − | |||
The position is a FreeCAD Vector <math>a \in \mathbb{R}^3</math>. The orientation is a FreeCAD rotation matrix. When we apply matrix <math>A</math> on vectors <math>x = (1,0,0)</math>, <math>y = (0,1,0)</math>, <math>y = (1,0,0)</math>, it creates vectors <math>x^*</math>, <math>y^*</math>, <math>y^*</math> such that | The position is a FreeCAD Vector <math>a \in \mathbb{R}^3</math>. The orientation is a FreeCAD rotation matrix. When we apply matrix <math>A</math> on vectors <math>x = (1,0,0)</math>, <math>y = (0,1,0)</math>, <math>y = (1,0,0)</math>, it creates vectors <math>x^*</math>, <math>y^*</math>, <math>y^*</math> such that | ||
* <math>x^*</math> points in the same direction as the port's normal, <math>x^* = n</math>. | * <math>x^*</math> points in the same direction as the port's normal, <math>x^* = n</math>. | ||
| Zeile 16: | Zeile 18: | ||
[[Datei:Port-orientation.svg|mini|Orientation of port 2 in a tee fitting.]] | [[Datei:Port-orientation.svg|mini|Orientation of port 2 in a tee fitting.]] | ||
| + | |||
==Adjust two fittings== | ==Adjust two fittings== | ||
When we adjust one fitting to another we want rotate the first fitting in such a way that its socket points in opposite directions as a socket of the other fitting. | When we adjust one fitting to another we want rotate the first fitting in such a way that its socket points in opposite directions as a socket of the other fitting. | ||
| − | Let us assume that the port of the adjusting fitting has position <math>a'</math>, orientation <math>A'</math> with normal <math>n'</math> and 0 degree reference <math>r'</math>. | + | Let us assume that the port of the adjusting fitting has position <math>a'</math>, orientation <math>A'</math> with normal <math>n'</math> and 0 degree reference <math>r'</math>. Everything refering to the local coordinates of the fitting. |
| − | The | + | |
| − | We want to find a rotation matrix <math>B</math>, such that | + | The other fitting has position <math>p</math> and rotation <math>R</math>. The local properties of its port has |
| − | * Its normal vector looks to opposite direction as the normal of the other fitting: <math>Bn'=- | + | has local position <math>a</math>, local orientation <math>A</math>, local normal <math>n</math> and local 0 degree reference <math>r</math>. |
| − | * Its zero-degree reference points to the same direction <math>Br'= | + | That means the corresponding global parameter of the port are |
| + | |||
| + | <math display="block"> | ||
| + | \begin{align} | ||
| + | a_g &:= p+Ra \\ | ||
| + | n_g &:= Rn \\ | ||
| + | r_g &:= Rr \\ | ||
| + | \end{align} | ||
| + | </math> | ||
| + | |||
| + | We want to find a rotation matrix <math>B</math> of the moved fitting, such that the new orientation of its port *in relating to global coordinate* has following properties: | ||
| + | * Its normal vector looks to opposite direction as the normal of the other fitting: <math>Bn'=-n_g</math>. | ||
| + | * Its zero-degree reference points to the same direction <math>Br'=r_g</math> | ||
We compose the matrix from three matrices <math>A'^{-1}</math><math>A_r</math> and <math>A</math>. | We compose the matrix from three matrices <math>A'^{-1}</math><math>A_r</math> and <math>A</math>. | ||
* <math>A'^{-1}</math> rotates the fitting in such a way that its port points to x-direction, and 0 reference to y-direction. | * <math>A'^{-1}</math> rotates the fitting in such a way that its port points to x-direction, and 0 reference to y-direction. | ||
* <math>A_r</math> rotates the fitting opposite to x-direction, but its 0 reference still points to y-direction. | * <math>A_r</math> rotates the fitting opposite to x-direction, but its 0 reference still points to y-direction. | ||
| − | * <math>A</math> | + | * <math>A</math> rotate oposite rotated port to the same direction as the port of the other fitting. |
| + | * <math>R</math> rotate to corresponding global rotation. | ||
| + | Note. Rotation operations are not commutative and we need to perform all the rotation from right to left. | ||
| + | We have <math display="block">B:= R \cdot A \cdot A_r \cdot A'^{-1}</math>. | ||
| + | |||
| + | == Ports in Python == | ||
| + | In ''OsePiping.Port'' class the port position and orientation are stored in the ''Port.placement'' attribute as a ''FreeCAD.Placement'' object. | ||
| − | + | The matrix <math>A_r</math> can be expressed as 180° rotation along the y axis: ''FreeCAD.Rotation(0, 180, 0)''. | |
Neueste Überarbeitung vom 2. Dezember 2018, 07:26 Uhr
Ports
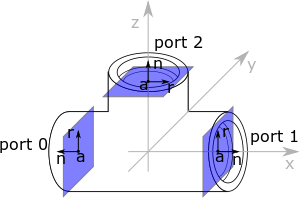
The OSE Piping Workbench creates fittings. It uses ports to describe the ends of the fittings. The Ports helps to fit the fittings together correctly.
Every port is described by:
- Its position .
- A normal vector which points out of the fitting and it is perpendicular to the port plane.
- A 0 reference angle vector it shows where is the degree 0°. must lie in the port plane.
All three vectors refer to local coordinates.
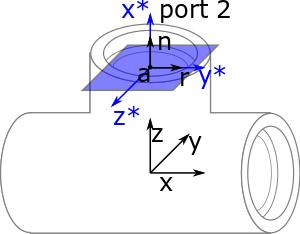
Instead of using three separate vectors, we represent the port by its position and its orientation .
The position is a FreeCAD Vector . The orientation is a FreeCAD rotation matrix. When we apply matrix on vectors , , , it creates vectors , , such that
- points in the same direction as the port's normal, .
- shows in the same direction as the angular reference, .
For example in a tee fitting, the matrix is a rotation along y-axis by , and then a rotation along z axis by . See FreeCAD Rotation for more details about rotation.
Adjust two fittings
When we adjust one fitting to another we want rotate the first fitting in such a way that its socket points in opposite directions as a socket of the other fitting. Let us assume that the port of the adjusting fitting has position , orientation with normal and 0 degree reference . Everything refering to the local coordinates of the fitting.
The other fitting has position and rotation . The local properties of its port has has local position , local orientation , local normal and local 0 degree reference . That means the corresponding global parameter of the port are
We want to find a rotation matrix of the moved fitting, such that the new orientation of its port *in relating to global coordinate* has following properties:
- Its normal vector looks to opposite direction as the normal of the other fitting: .
- Its zero-degree reference points to the same direction
We compose the matrix from three matrices and .
- rotates the fitting in such a way that its port points to x-direction, and 0 reference to y-direction.
- rotates the fitting opposite to x-direction, but its 0 reference still points to y-direction.
- rotate oposite rotated port to the same direction as the port of the other fitting.
- rotate to corresponding global rotation.
Note. Rotation operations are not commutative and we need to perform all the rotation from right to left. We have
Ports in Python
In OsePiping.Port class the port position and orientation are stored in the Port.placement attribute as a FreeCAD.Placement object.
The matrix can be expressed as 180° rotation along the y axis: FreeCAD.Rotation(0, 180, 0).