Naives Entscheidungsmodell: Unterschied zwischen den Versionen
Ruslan (Diskussion | Beiträge) (text korrigiert) |
Ruslan (Diskussion | Beiträge) (Rechtschreibung) |
||
| Zeile 128: | Zeile 128: | ||
=== Intuitive Ergebnisse === | === Intuitive Ergebnisse === | ||
| − | Viele Ergebnisse aus dem Modell sind intuitiv. Das ist schön - sie zeigen, dass das Model plausibel ist. Doch vorsichtig! Vetraue nie deiner Intuition bei | + | Viele Ergebnisse aus dem Modell sind intuitiv. Das ist schön - sie zeigen, dass das Model plausibel ist. Doch vorsichtig! Vetraue nie deiner Intuition bei den stochastischen Problemen. Stochastik ist kontraintuitiv, desswegen muss man alle Ergebnisse formal begründen. Hier sind diese Ergebnisse: |
"Wenn man nur begrenze Anzahl der Personen befragen kann, frag die schlauesten Menschen." | "Wenn man nur begrenze Anzahl der Personen befragen kann, frag die schlauesten Menschen." | ||
| Zeile 142: | Zeile 142: | ||
"Wer häufig daneben liegt, ist genau so wichtig wie ein Experte! Fragt ihn/sie und tu das Gegenteil." | "Wer häufig daneben liegt, ist genau so wichtig wie ein Experte! Fragt ihn/sie und tu das Gegenteil." | ||
| − | Begründung <math>p_i/(1-p_i)</math> ist genau dann maximal wenn <math>(1-p_i)/p_i</math> minimal ist. | + | Begründung <math>p_i/(1-p_i)</math> ist genau dann maximal, wenn <math>(1-p_i)/p_i</math> minimal ist. |
| − | Wir nennen diese | + | Wir nennen diese extraordinäre Menschen mit <math>p_i < 1/2</math> – "Antiexperten" 😁. |
| − | Schlussfolgerung: Das wichtigste ist herauszufinden wer ein Antiexperte ist. | + | Schlussfolgerung: Das wichtigste ist es, herauszufinden, wer ein Antiexperte ist. |
| − | Jede Meinung | + | Jede Meinung mit <math>p_i > 1/2</math> ist wichtig. Wenn man Gegenteil von Antiexperten tut, konwertiert man jede Entscheidung in <math>p_i > 1/2</math>. |
"Manchmal weiß eine Person mit viel Erfahrung ''weniger'' als zwei Personen mit wenig Erfahrung." | "Manchmal weiß eine Person mit viel Erfahrung ''weniger'' als zwei Personen mit wenig Erfahrung." | ||
| Zeile 158: | Zeile 158: | ||
</math> | </math> | ||
| − | Wenn zwei weniger Erfahrene | + | Wenn zwei weniger Erfahrene gleiche Erfolgrswahrscheinlichkeiten <math>p_1 = p_2</math> haben, gilt für die obere Formel: |
<math display="block"> | <math display="block"> | ||
\begin{array}{rrl} | \begin{array}{rrl} | ||
| Zeile 166: | Zeile 166: | ||
\end{array} | \end{array} | ||
</math> | </math> | ||
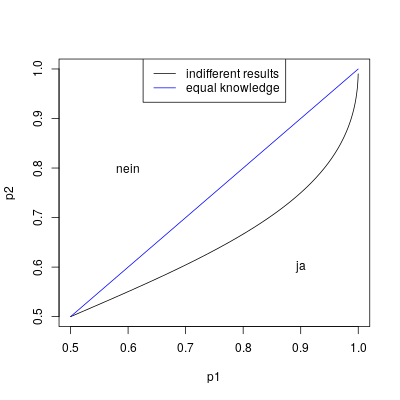
| − | Der Graph unten zeigt, wenn die Meinung "ja" der ersten Person | + | Der Graph unten zeigt, wenn die Meinung "ja" der ersten Person gleich wichtig ist, wie die Meinungen "nein" der anderen beiden Personen. Das sind alle Punkten unterhalb der Linie. |
| − | Die gerade blaue Linie | + | Die gerade blaue Linie zeigt, wenn alle gleiches Wissen haben, d.h. <math>p_1 = p_2 = p_3 </math>. Man kann aus diesem Graphen schlussfolgern: |
* Wenn ein wirklich guter Experte (<math>p_1</math> sehr nah an 1) "ja" sagt, dann muss man wirklich gut sein (<math>p_2</math> und <math>p_3</math> auch nahe 1) und diese Meinung mit "nein" überstimmen. | * Wenn ein wirklich guter Experte (<math>p_1</math> sehr nah an 1) "ja" sagt, dann muss man wirklich gut sein (<math>p_2</math> und <math>p_3</math> auch nahe 1) und diese Meinung mit "nein" überstimmen. | ||
| − | * Wenn man kein wirklich guter Experte ist (<math>p_1</math> nicht nah an 1) und | + | * Wenn man kein wirklich guter Experte ist (<math>p_1</math> nicht nah an 1) und "ja" sagt, dann reichen zwei weniger Erfahrene aus, um diese Antwort mit "nein" zu überstimmen. |
[[Datei:Indifference-plot.png]] | [[Datei:Indifference-plot.png]] | ||
Version vom 30. März 2019, 11:28 Uhr
Warnung
Es ist sehr einfach in einem stochastischen Modell Fehler zu machen. Hier sind nur meine vorläufigen Ergebnisse.
Problem
Wie kann OSEG entscheiden, ein Projekt zu unterstützen oder nicht?
Die Antwort ist doch klar: wir nutzen unser gesamtes Wissen – wir machen eine Umfrage. Nun sind nicht alle Menschen Experten in Allem. Wie machen wir diese Umfrage so geschick, dass die Antwort möglichst richtig ist? Diese Frage möchten wir hier beantworten.
Unswer Hauptwerkzeug ist mathematische Modellierung mit sehr einfachen Modellen. Auch wenn die Realität sehr komplex ist, können wir aus einfachen Beispielen viel lernen.
Hintergrund
Diese Aufgabe entstand während des Hackathons 2019. Problem: Eine Gruppe von OSEG soll entscheiden ob OSEG ein Projekt mit offiziell unterstüzt. Moe hat ein Verfahren dazu vorgeschlagen: Umfrage von OSEG nicht Experten, OSEG Experten und speizeillen OSEG Leuten damit alles rechtlich korrekt ist.
Ich werde hier mein naives mathematisches Modell dazu erstellen. Es ist naiv, weil ich kein Experte auf diesem Gebiet bin – welch eine Ironie 😬. Ich werde hier zuerst meine Fragen und Annahmen sammeln und dann gucken, was Profis dazu sagen.
Mathematisches Modell
Unser Problem soll möglichst einfach sein. Wir gehen von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle n} Menschen aus. Alle diese Menschen haben unterschiedlichen Wissenstand. Sie müssen eine Frage mit "ja" oder "nein" beantworten. Diese Antwort kann objektiv korrekt oder falsch sein. Wir müssen diese Antworten so schlau kombinieren, dass unser Ergebnis so korrekt wie möglich ist.
Mensch
Wir modellieren jeden Menschen durch eine Zufallsvariable Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle X_i} , Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle i \in = \{1, ,\ldots, n\}} . Jeder Mensch beantwortet eine Frage mit "ja" oder "nein". Das bedeutet Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle X_i \in \{ja,nein\}} . Wir nehmen an, dass die Menschen, die Fragen unabhänging von einenader beantworten.
Wirklichkeit
Wir modellieren die Wirklichkeit, als eine Zufallsvariable Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle W \in \{ja,nein\}} . Sie repräsentiert die richtige Antwort "ja" oder "nein". Bevor wir Menschen fragen, haben wir überhaupt keine Ahnung, was die richtige Antwort ist, daher gilt für die Wahrscheinlichkeit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle P(W =ja)=P(W =nein)=1/2} .
Wissen
Jeder Mensch hat unterschiedliches Wissen. Das drücken wir durch unterschiedliche Wahrscheinlichkeiten, die richtige Antwort zu erraten Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle p_i:= P(X_i =ja|W =ja):=P(X_i = nein|W = nein).} Hier haben wir gleichzeitig angenommen, dass der Mensch gleich gut eine "nein"- und eine "ja"-Antwort erraten kann.
Weil die Menschen unabhängig von einenader die Frage beantworten, gilt für jede Untermenge[1] Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle I \subset \{1,\ldots,n\}} Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{align} P\big(\bigcap_{i \in I} X_i =ja |W =ja\big)&=\prod_{i \in I} P(X_i = ja|W = ja)\\ P\big(\bigcap_{i \in I} X_i =ja |W =nein\big)&=\prod_{i \in I} P(X_i = ja|W = nein). \end{align} }
Entscheidung basierend auf einer Umfrage
Unsere Entscheidung ist eine Funktion Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f(p_1,\ldots,p_n, x_1,\ldots,x_n,m)} .
- Parametren Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle (p_1,\ldots,p_n)}
- Sie hängt von den Menschen Entscheidungen (x_1,\ldots,x_n) "ja" oder "nein".
- Einem Münzenwurf Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle m \in \{ja, nein\}} , wenn sie unentschieden ist.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{rrcl} f&:[0,1]^n\times {\{ja,nein}\}^{(n+1)} & \longrightarrow &\{ja,nein\} \\ &(p_1,\ldots,p_n, x_1,\ldots,x_n,m)& \mapsto &f(p_1,\ldots,p_n, x_1,\ldots,x_n,m) \end{array} }
Die Entscheidungen aller Menschen können wir mit einer Menge Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle J \subset \{1,\ldots,n\} } ausdrücken. Diese Menge enthält alle Indizes, die die Frage mit "ja" beantwortet haben. Das Komplement dieser Menge Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle J^c} in Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \{1,\ldots,n\} } representiert die "nein"-Entscheidungen.
Mathematische Lösung
Nachdem alle Menschen ihre Antworten gegeben haben, können wir berechnen mit welcher Wahrscheinlichkeit die Reailtät auch mit "ja" antwortet: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle P(\text{richtige Antwort ja}) = P\big(W=ja|\bigcap_{i \in J} X_i = ja, \bigcap_{i \in J^c} X_i = nein\big).} Mit Bayes Formula gilt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle P\big(W=ja|\bigcap_{i \in J} X_i = ja, \bigcap_{i \in J^c} X_i = nein\big) = \frac{ P(\bigcap_{i \in J} X_i = ja, \bigcap_{i \in J^c} X_i = nein|W=ja)\cdot P(W=ja) }{ P(\bigcap_{i \in J} X_i = ja, \bigcap_{i \in J^c} X_i = nein|W=ja)\cdot P(W=ja) + P(\bigcap_{i \in J} X_i = ja, \bigcap_{i \in J^c} X_i = nein|W=nein)\cdot P(W=nein) }. }
Wir kürzen überall Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle P(W=nein) = P(W=nein) = 1/2 } , dann gilt
Jetzt setzen wird die definierten Wahrscheinlichkeiten für richtige Antworten und damit Wahrscheinlichkeiten für falsche Antworten ein und erhalten
Uns interessiert, ob diese Wahrscheinlichkeit größer ist als die Wahrscheinlichkeit für eine falsche Antwort. Das ist
Also wenn gilt
Unsere Entscheidungsfunktion ist somit:
Interpretation der Lösung
Intuitive Ergebnisse
Viele Ergebnisse aus dem Modell sind intuitiv. Das ist schön - sie zeigen, dass das Model plausibel ist. Doch vorsichtig! Vetraue nie deiner Intuition bei den stochastischen Problemen. Stochastik ist kontraintuitiv, desswegen muss man alle Ergebnisse formal begründen. Hier sind diese Ergebnisse:
"Wenn man nur begrenze Anzahl der Personen befragen kann, frag die schlauesten Menschen."
TODO: formale Begründung aufschreiben.
"Frag soviele Menschen wie möglich".
TODO: Formale Begründung aufschreiben.
Wenig intuitive Ergebnisse
"Wer häufig daneben liegt, ist genau so wichtig wie ein Experte! Fragt ihn/sie und tu das Gegenteil."
Begründung ist genau dann maximal, wenn minimal ist.
Wir nennen diese extraordinäre Menschen mit – "Antiexperten" 😁.
Schlussfolgerung: Das wichtigste ist es, herauszufinden, wer ein Antiexperte ist. Jede Meinung mit ist wichtig. Wenn man Gegenteil von Antiexperten tut, konwertiert man jede Entscheidung in .
"Manchmal weiß eine Person mit viel Erfahrung weniger als zwei Personen mit wenig Erfahrung." "Manchmal weiß eine Person mit viel Erfahrung mehr als zwei Persone nmit wenig Erfahrung."
Wir nummerieren die Menschen mit 1 für viel Erfahrung und 2, 3 mit wenig Erfahrung. Wir befragen sie. Wenn 1 sagt "Ja" aber 2 und 3 sagen "nein", wir wählen "ja" nur wenn
Wenn zwei weniger Erfahrene gleiche Erfolgrswahrscheinlichkeiten haben, gilt für die obere Formel:
- Wenn ein wirklich guter Experte ( sehr nah an 1) "ja" sagt, dann muss man wirklich gut sein ( und auch nahe 1) und diese Meinung mit "nein" überstimmen.
- Wenn man kein wirklich guter Experte ist ( nicht nah an 1) und "ja" sagt, dann reichen zwei weniger Erfahrene aus, um diese Antwort mit "nein" zu überstimmen.
Implementatierung
R implementatirung
# "Yes" is 1, "No" is 0.
decide<-function(p, w){
# p are probabilities for correct answer.
# x are results of a survey.
# Invert x when p < 1/2.
x[p<0.5]<-!x[p<0.5]
if(result_consitant(p,x)){
m <- rbinom(10, 1, prob=0.5)
return(f(p,x, m))
}else{
stop("Inconsistant results: two different answers are possible.")
}
}
result_consitant<-function(p,x){
# A reasult is NOT consitant, when two persons who are always right but
# give different answers
sure_events = unique(x[p]==1)
return (length(sure_events)<=1)
}
f<-function(p,x,m){
pos<-positive(x,p)
if(pos > 0.5){
return(1)
}else if(pos < 0.5){
return(0)
}else{
return(m)
}
}
positive<-function(x,p){
# Return probability for the positive_answer.
a <- prod(p[x])*prod((1-p)[!x])
b <- prod((1-p)[x])*prod(p[!x])
return(a/(a+b))
}
p <- c(0.9, 0.7, 0.7)
x <- c(1,0,0) # Opinions are "Yes", "No", "No".
decide(p, x) # Decision is "Yes".
p <- c(0.84, 0.7, 0.7)
decide(p, x) # Decision is "No".
Referenzen
Youtube Kanal von Nikolai Osipov (Николай Николаевич Осипов), über kollektive Intelligenz. https://www.youtube.com/channel/UCuH_xeNX7KKIYHeZXaPO_OA
Notizen
"ja" und "nein" vs "richtig" und "falsch"
Mein erstes Modell war nicht mit "ja" und "nein" sondern mit "richtig" und "falsch". Dieses Modell verleiht dazu, eine Entscheidungsfunktion zu konstruieren die immer "richtig" ist, ohne die Antworten von Experten zu berücksichtigen. Das ist zu unrealistisch. Ich werde später mir dieses Modell nochmal ansehen und Zusammenhang zu dem "ja"-"nein"-Modell analysieren.
Fast keine Ahnung ist auch gut
Ich habe ein Gefühl, dass "Fast keine Ahnung"-Leute, das sind Leute mit , sehr wichtig sind. Vielleicht senken sie gut die Varianz der Entscheidungsfunktion auf Grund des Gesetzes der Großen Zahlen.
- ↑ Ich wähle eine Untermenge, weil man in Wahrscheinlichkeitstheorie zwischen einer Unabhängigkeit und einer paarweisen Unabhängigkeit unterscheiden muss. Es ist ausreichend, nurdie "ja" Antworten zu betrachten, weil es ist ein Erzeuger von der -Algebra erzeugt durch alle Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \sigma (X_i)_{1 \leq i \leq n}} bedingt durch Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle W=ja} bzw. Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle W=nein} .