Naives Entscheidungsmodell
Problem
Wie kann OSEG entscheiden ein Projekt zu unterstützen oder nicht?
Die Antwort ist doch klar: wir nutzen unser gesamtes Wissen, wir machen eine Umfrage. Nun sind nicht alle Menschen Experten in Allem. Wie machen wir diese Umfrage so geschickt, dass die Antwort möglichst richtig ist? Diese Frage möchten wir hier beantworten. Und wir müssen auch berücksichtigen dass diese Vorgehensweise technisch möglich ist.
Hintergrund
Diese Aufgabe entstand beim Hackathon 2019. Moe hat ein Verfahren für die Projekt Unterstützung vorgeschlagen. Ich werde hier erstmal mein naives mathematisches Modell dazu erstellen. Es ist naiv, weil ich kein Experte in diesen Aufgaben bin -- welch eine Ironie 😬. Ich werde hier zuerst meine Fragen und Annahmen sammeln und dann gucken was Profis dazu gesagt haben.
Einfaches Problem
Unser model soll zuerst möglichst einfach sein. Wir gehen von Menschen aus. Alle diese Menschen haben unterschiedlichen Wissenstand. Sie müssen eine Frage mit "ja" oder "nein" beantworten. Diese Antwort kann objektiv korrekt oder falsch sein. Wir müssen diese Antworten so schlau kombinieren, dass unser Ergebnis so korrekt wie möglich ist.
Mathematisches Modell
Mensch
Wir modellieren jeden Menschen durch eine Zufallsvariablen , . Jeder Mensch beantwortet eine Frage mit "ja" oder "nein". Das bedeutet . Um das Modell zu vereinfachen, nehmen wir an, dass die Menschen, die Fragen unabhänging von einenader beantworten.
Wirklichkeit
Wir modellieren die Wirklichkeit, als eine Zufallsvariable Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle W \in \{ja,nein\}} . Sie repräsentiert die richtige Antwort "ja" oder "nein". Bevor wir Menschen fragen, haben wir überhaupt keine Ahnung, was die richtige Antwort ist, daher gilt für die Wahrscheinlichkeit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle P(W =ja)=P(W =nein)=1/2} .
Wissen
Jeder Mensch kann unterschiedliches Wissen haben. Das Drucken wir durch unterschiedliche Wahrscheinlichkeit die richtige Antwort zu erraten. Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle p_i:= P(X_i =ja|W =ja):=P(X_i = nein|W = nein)} Hier haben wir gleichzeitig eine Annahme gemacht, dass der Mensch gleich gut eine "nein" und eine "ja" Antwort erraten kann.
Weil die Menschen unabhängig von einenader die Frage beantworten gilt für jede Untermengen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle I \subset \{1,\ldots,n\}} Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle P(\bigcap_{i \in I} X_i =ja |W =ja):=\prod_{i \in I} P(X_i = nein|W = nein) }
Entscheidung basierend auf einer Umfrage
Unsere Entscheidung ist eine Funktion Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f(x_1,\ldots,x_n)} , die von den Menschen Entscheidungen abhängig ist und eine Antwort "ja" oder "nein" zurück gibt.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{rcl} f:{\{ja,nein}\}^n & \longrightarrow &\{ja,nein\} \\ (x_1,\ldots,x_n) & \mapsto &f(x_1,\ldots,x_n) \end{array} }
Die Entscheidungen aller Menschen können wir mit einer Menge Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle J \subset \{1,\ldots,2\} } ausdrücken. Diese Menge enthält alle Indizes, die die Frage mit "ja" beantwortet haben. Das Komplement dieser Menge Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle J^c \subset \{1,\ldots,2\} } representiert die "nein"-Entscheidungen.
Mathematische Lösung
Nachdem alle Menschen ihre Antworten gegeben haben, können wir berechnen mit welcher Wahrscheinlichkeit deren Antwort "ja" ist: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle P(richtige Antwort) = P(W=ja|\bigcap_{i \in J} X_i = ja, \bigcap_{i \in J^c} X_i = nein).} Mit Bayes Formula gilt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle P(W=ja|\bigcap_{i \in J} X_i = ja, \bigcap_{i \in J^c} X_i = nein) = \frac{ P(\bigcap_{i \in J} X_i = ja, \bigcap_{i \in J^c} X_i = nein|W=ja)\cdot P(W=ja) }{ P(\bigcap_{i \in J} X_i = ja, \bigcap_{i \in J^c} X_i = nein|W=ja)\cdot P(W=ja) + P(\bigcap_{i \in J} X_i = ja, \bigcap_{i \in J^c} X_i = nein|W=nein)\cdot P(W=nein) }. }
Wir können überall kürzen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle P(W=nein) = P(W=nein) = 1/2 } Dann gilt
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle P(W=ja|\bigcap_{i \in J} X_i = ja, \bigcap_{i \in J^c} X_i = nein) = \frac{ P(\bigcap_{i \in J} X_i = ja, \bigcap_{i \in J^c} X_i = nein|W=ja) }{P(\bigcap_{i \in J} X_i = ja, \bigcap_{i \in J^c} X_i = nein|W=ja)+P(\bigcap_{i \in J} X_i = ja, \bigcap_{i \in J^c} X_i = nein|W=nein) }. } Dadurch, dass die Menschen unabhängign von einander die Etscheidungen treffen gilt:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle P(W=ja|\bigcap_{i \in J} X_i = ja, \bigcap_{i \in J^c} X_i = nein) = \frac{\prod_{i \in J} P(X_i = ja|W=ja) \prod_{i \in J^c}P(X_i = nein|W=ja) }{\prod_{i \in J} P(X_i = ja|W=ja) \prod_{i \in J^c}P(X_i = nein|W=ja) +\prod_{i \in J} P(X_i = ja|W=nein) \prod_{i \in J^c}P(X_i = nein|W=nein) }. }
Jetzt setzen wird die definierte Wahrscheinlichkeiten für richtige Antworten Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle P(X_i=ja | W=ja) = P(X_i=nein | W=nein) = p_i } und die damit Wahrscheinlichkeiten für falschen Antworten Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle P(X_i=nein | W=ja) = P(X_i=ja | W=nein) = 1-p_i } und erhalten
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle P(W=ja|\bigcap_{i \in J} X_i = ja, \bigcap_{i \in J^c} X_i = nein) = \frac{\prod_{i \in J} p_i \prod_{i \in J^c}(1-p_i) }{\prod_{i \in J} p_i \prod_{i \in J^c}(1-p_i) + \prod_{i \in J}(1- p_i) \prod_{i \in J^c}p_i }. }
Uns interessiert, wenn diese Wahrscheinlichkeit größer ist als die Wahrscheinlichkeit für eine falsche Antwort. Das ist dann
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle P(\text{ja richtige Antwort}) > P(\text{ja falsche Antwort}) \Leftrightarrow P(\text{ja richtige Antwort}) > 1- P(\text{ja richtige Antwort}) \Leftrightarrow P(\text{ja richtige Antwort}) > 1/2.}
Also wenn gilt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{rrl} & \frac{\prod_{i \in J} p_i \prod_{i \in J^c}(1-p_i) }{\prod_{i \in J} p_i \prod_{i \in J^c}(1-p_i) + \prod_{i \in J}(1- p_i) \prod_{i \in J^c}p_i } & > 1/2 \\ \Longleftrightarrow & \prod_{i \in J} p_i \prod_{i \in J^c}(1-p_i) & > \prod_{i \in J}(1- p_i) \prod_{i \in J^c}p_i. \end{array} } oder Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{rrl} \Longleftrightarrow & \prod_{i \in J} \frac{p_i}{1-p_i} \prod_{i \in J^c}\frac{1-p_i}{p_i} & > 1. \end{array} }
Unsere Entscheidungsfunktion ist somit:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f:(x_1,\ldots,x_n) = \begin{cases} ja & \text{wenn } \prod_{i \in J} p_i \prod_{i \in J^c}(1-p_i) > \prod_{i \in J}(1- p_i) \prod_{i \in J^c}p_i \\ nein & \text{wenn } \prod_{i \in J} p_i \prod_{i \in J^c}(1-p_i) < \prod_{i \in J}(1- p_i) \prod_{i \in J^c}p_i \\ \text{eine Münze werfen} & \text{sonst} \end{cases} }
Interpretation der Lösung
intuitive Ergebnisse
Viele Ergebnisse aus dem Modell sind intuitiv. Das ist schön - sie zeigen, dass das Model plausibel ist. Doch vorsichtig! Vetraue nie deiner Intuition bei der Lösung der stochastischen Problemen. Stochastik ist kontraintuitiv, desswegen muss man alle Ergebnisse formal begründen. Hier sind diese Ergebnisse:
"Wenn man nur begrenze Anzahl der Personen befragen kann, frag die schlauesten Menschen."
Begründung "Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle h} (TODO: noch zu definierien) ist maximal wenn Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle p_i} maximal sind." (für alle Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle p_i \geq 1/2} )
"Frag soviele Menschen wie möglich".
TODO: Formale Begründung aufschreiben.
wenig intuitive Ergebnisse
"Wer häufig daneben liegt, ist ein Experte! Fragt ihn/sie und tu das Gegenteil."
Begründung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle p_i/(1-p_i)} ist genau dann maximal wenn Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle (1-p_i)/p_i} minimal ist.
"Manchmal eine Person mit viel Erfahrung weiß **weniger** als zwei Personen mit wenig Erfahrung."
"Manchmal eine Person mit viel Erfahrung weiß **mehr** als zwei Persone nmit wenig Erfahrung."
Wir nummerieren die Mensche mit 1 für viel Erfahrung und 2, 3 mit wenig Erfahrung. Wir befragen sie. Wenn 1 sagt "Ja" aber 2 und 3 sagen "nein", wir wählen "ja" nur wenn
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle p_1 \cdot (1-p_2)\cdot (1-p_3) > (1-p_1) \cdot p_2 \cdot p_3. }
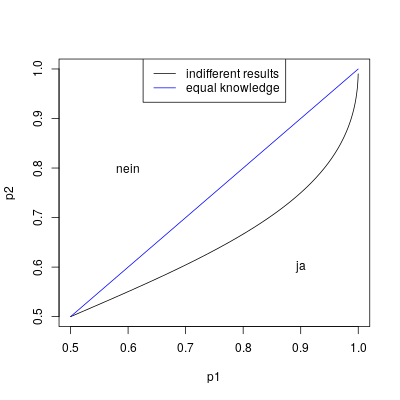
Wenn zwei weniger Erfahrene haben gleiche Erfolgrswahrscheinlichkeiten Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle p_1 = p_2} wir wählen "Ja" nur wenn gilt: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{rrl} &p_1 \cdot (1-p_2)^2 &> (1-p_1) \cdot p_2^2 \\ \Longleftrightarrow & p_1 ((1-p_2)^2 + p_2^2) &> \cdot p_2^2 \\ \Longleftrightarrow & p_1 &> \frac{p_2^2}{(1-p_2)^2 + p_2^2}. \end{array} } Der Graph unten zeigt, wenn die Meinung "ja" der ersten Person, ist "gleich wichtig" als die Meinungen "nein" der anderen beiden Personen. Das sind alle Punkten unterhalb der Linie.
Notizen
"ja" und "nein" vs "richtig" und "falsch"
Mein erstes Modell war nicht mit "ja" und "nein" sondern mit "richtig" und "falsch". Dieses Modell verleiht dazu, eine Entscheidungsfunktion zu konstruieren die immer "richtig" ist, ohne die Antworten von Experten zu berücksichtigen. Das ist zu unrealistisch. Ich werde später mir dieses Modell nochmal ansehen und Zusammenhang zu dem "ja"-"nein"-Modell analysieren.