Einführung in die Dielektrizität & Kapazität (Eric P. Dollard)

Quelle: Artikel von Eric P. Dollard in The Journal of Borderland Research [Die Zeitschrift für Grenzbereich Forschung] (1990), Bd. 46, Nr. 02, siehe https://borderlandsciences.org/journal/vol/46/n02/Dollard_on_Dielectricity_Capacitance.html
Übersetzung: Andreas Plank

Schlüsselwörter: Kapazität, Strom, Dielektrizität, elektrisches Feld, Faraday, Steinmetz, Tesla, Theorie, Stromspannung, Magnetismus, Energie, falsche Konzeption

Kapazität

Das Kapazitätsphänomen ist eine Art der elektrischen Energiespeicherung in der Form eines Feldes in einem umgrenzten Raum. Dieser Raum ist in der Regel durch zwei parallele metallische Platten beschränkt oder zweier metallischer Folien auf einem dazwischenliegenden Isolator oder Dielektrikum. Kapazität kann eine schier unendliche Vielfalt an komplexeren Strukturen aufweisen, solange ein Unterschied im elektrischen Potential zwischen den verschiedenen Flächen der Struktur existiert. Die oszillierende Spule stellt eine Möglichkeit, als ein Kondensator komplexer Form, dar und diese wird hier präsentiert.

Kapazität unzureichend erklärt

Die Auffassung der Kapazität die heutzutage angewendet wird, ist vollkommen ungeeignet für das richtige Verständnis dieses Effekts. Steinmetz erwähnt dies in seinem einführenden Buch Elektrische Entladungen, Wellen und Impulse. Zitat [ S. 13 ], Unglücklicherweise, ist beim Umgang mit dielektrischen Feldern zum großen Teil noch die prähistorische Konzeption der elektrostatischen Ladung (Elektron) auf dem Stromleiter vorhanden, und durch deren Gebrauch zerstört es die Entsprechung zwischen den beiden Komponenten des elektrischen Feldes, der magnetischen und dielektrischen, und macht die Erwägung dielektrischer Felder unnötig kompliziert.

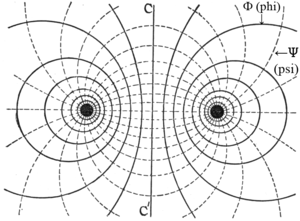
Abb. 1a — Elektrisches Feld eines Stromkreises. [ Φ magnetischer Fluss; Ψ dielektrischer Fluss; aus Steinmetz (1911, S.11) ]

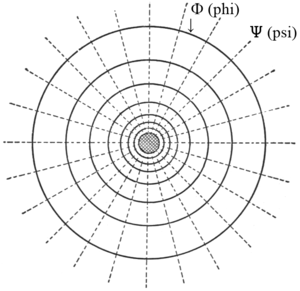
Abb. 1b — Elektrisches Feld eines Stromleiters. [ Φ magnetischer Fluss; Ψ dielektrischer Fluss; aus Steinmetz (1911, S.11) ]

Kraftlinien als Darstellung der Dielektrizität

Steinmetz führt weiter aus [ S. 14 ], Es ist offensichtlich nicht sinnvoller, wenn man den Kapazitätsstrom als Strom denkt, der den Leiter mit einer Menge Elektrizität auflädt, als wenn man von der Induktionsspannung spricht, die den Leiter mit einer Menge Magnetismus auflädt. Aber die letztgenannte Konzeption, zusammen mit der Vorstellung einer Menge an Magnetismus, etc., verschwand seit Faradays Darstellung des magnetischen Feldes mittels Kraftlinien.

Die Gesetze der Kraftlinien

Alle Linien der magnetischen Kraft sind in sich selbst geschlossen, alle dielektrischen Kraftlinien enden auf Stromleitern, aber können geschlossene Schleifen in elektromagnetischer Strahlung bilden. Diese stellen die grundlegenden Gesetze der Kraftlinien dar. Man kann anhand dieser Gesetze sehen, dass jede Kraftlinie nicht einfach im Raum enden kann.

Faraday & Kraftlinien-Theorie

Faraday war überzeugt, dass die Fernwirkung nicht durch leeren Raum möglich ist, oder mit anderen Worten [ S.293 in „Experimentelle Forschungen in der Elektrizität“ Bd.3 ], Materie kann nicht wirken, wo sie nicht ist. Er erachtete Raum als von Linien der Kraft durchzogen. Fast jeder ist vertraut mit den Mustern, die durch Eisenspäne um einen Magneten geformt werden. Diese Späne wirken als zahlreiche kleine Kompasse und orientieren sich entlang der bestehenden Feldlinien rund um die Pole des Magneten. Experimentieren hat gezeigt, dass ein Magnetfeld eine faserige Konstruktion besitzt. Indem eine Drahtspule ein starkes Magnetfeld passiert und durch belauschen des Spulenausgangs mittels Kopfhörer, wird der Experimentator ein kratzendes Geräusch feststellen. J. J. Thompson führte weitere Experimente mit der Ionisation von Gasen durch, die zeigen, dass das Feld nicht kontinuierlich, sondern faserartig ist (ELEKTRIZITÄT UND MATERIE, 1904).

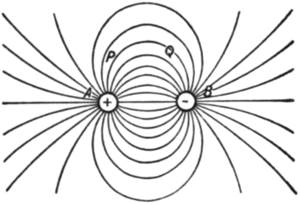
Abb. 2 [ Elektrische Körper mit gleichwertigen, aber entgegengesetzten Ladungen; aus Thomson (1904, S.10) ]

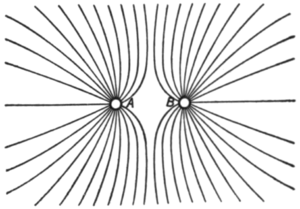
Abb. 3 [ Elektrische Körper mit gleichen Ladungen; aus Thomson (1904, S.11) ]

Physikalische Eigenschaften von Kraftlinien

Betrachte den Raum zwischen den Polen eines Magneten oder Kondensators als Fülle an Linien elektrischer Kraft. Siehe Abb. 1. Diese Kraftlinien wirken als eine Menge an gedehnten und sich gegenseitig abstoßend Federn. Jeder, der die Pole zweier Magneten zusammengedrückt hat, hat diese federnde Masse gefühlt. Beobachten wir Abb. 2. Beachte die dichteren Linien der Kraft entlang AB zwischen den Polen, und dass mehr Linien an A B zugewandt sind als nach außen in die Unendlichkeit hinausragen. Betrachte nun die Effekte der Kraftlinien an A. Diese Linien sind in einem Zustand der Spannung und ziehen an A. Weil mehr an A in Richtung B zurück ziehen, als diejenigen, die an A weg von B ziehen, haben wir die Phänomene der physikalischen Anziehung. Jetzt beobachten wir Abb. 3. Beachte nun, dass die Pole eher gleichartig sind statt ungleichartig, mehrere oder alle Linien ziehen A von B weg; die Phänomene der physikalischen Abstoßung.

Masse im Zusammenhang mit Kraftlinien in Bewegung

Die Kraftlinie kann man klarer verstehen, wenn man sie als ein Krafttubus oder einen langen, dünnen Zylinder abbildet. Maxwell stellte die Idee vor, die Gespanntheit eines Krafttubus ist repräsentativ für die elektrische Kraft (Volt/Zoll), und zusätzlich zu dieser Gespanntheit, gibt es ein Medium, durch das diese Tubusse passieren. Es gibt einen hydrostatischen Druck gegen das Medium oder den Äther. Der Wert dieses Druckes ist die Hälfte des Produkts aus dielektrischer und magnetischer Dichte. Dann gibt es Druck im rechten Winkel zu einem elektrischen Krafttubus. Wenn durch das Anwachsen eines Feldes sich der Krafttubus seitwärts oder in der Weite ausbreitet, stellt das Ziehen der Breitseite durch das Medium die magnetische Reaktion auf das Wachstum an Intensität des elektrischen Stroms dar. Jedoch, wenn ein Krafttubus dazu gebracht wird, sich zum Ende zu bewegen, wird er durch das Medium gleiten mit wenig oder gar keinem Ziehen, da wenig Angriffsfläche geboten wird. Dies erklärt möglicherweise, warum bei bestimmten Experimenten von Tesla kein Magnetfeld assoziiert ist, die Bewegung an Energie zum Gegenstand haben ohne begleitendes magnetisches Feld.

Induktivität als eine Analogie zur Kapazität

Viel von dem Geheimnis um die Funktionsweise der Kapazität kann geklärt werden, durch genaue Untersuchung der Induktivität und wie es dielektrische Phänomene hervorrufen kann. Induktivität stellt Energiespeicherung im Raum dar als einem magnetischen Feld. Die Kraftlinien orientieren sich in engen Schleifen rund um die Achse des Stromflusses, der sie hervorgebracht hat. Je größer der Raum zwischen diesem Strom und dessen Abbilder oder Spiegelungen, desto mehr Energie kann im resultierenden Feld gespeichert werden.

Mechanismus der magnetischen Energiespeicherung

Der Prozess diese Linien oder Schleifen nach außen zu drängen, stellt die Speicherung an Energie wie im Gummiband dar. Eine vorgegebene Stärke an Strom wird eine Kraftschleife in einem bestimmten Abstand zum Leiter halten durch den der Strom fließt, daher keine Energiebewegung. Wenn der Stromfluss erhöht wird, wird Energie durch das Feld absorbiert weil die Schleifen dann bei einer entsprechenden Geschwindigkeit nach außen gedrängt werden. Weil Energie in Bewegung ist, muss eine E. M. K. [ Elektromotorische Kraft ] den Stromfluss begleiten, um sich damit als Kraft abzubilden. Das Ausmaß dieser EMK entspricht exakt der Geschwindigkeit des Feldes. Wenn dann der Strom aufhört, seine Größe zu ändern und dadurch konstant wird, begleitet ihn keine EMK, da keine Energie absorbiert wird. Wenn jedoch der Strom abnimmt und dann eine negative Geschwindigkeit des Feldes darstellt, ziehen sich die Schleifen zusammen. Da die EMK genau der Geschwindigkeit entspricht, kehrt sie die Polarität um und kehrt dadurch die Kraft um, so dass sie sich nun aus dem Feld und in den Strom bewegt. Da keine Energie benötigt wird, um ein Feld aufrechtzuerhalten, repräsentiert nur der Strom, das statische oder stationäre Feld, gespeicherte Energie.

Die Grenzen von Null und Unendlich

Viele interessante Merkmale der Induktivität manifestieren sich selbst in den zwei Grenzfällen, bei denen die Energie eingefangen oder sofort freigesetzt wird. Da die Stromversorgung, die den Strom antreibt, einen Widerstand aufweist, leitet die Induktivität beim Abschalten ihre Energie in diesen Widerstand ab, der sie in Form von Wärme zusammenbringt. Wir werden eine perfekte Induktivität annehmen, die keinen Eigenwiderstand hat. Wenn wir die Stromversorgung durch Kurzschließen der Anschlüsse des Induktors entfernen, haben wir sie isoliert, ohne irgendeinen Strom zu unterbrechen. Da der Zusammenbruch des Feldes eine EMK erzeugt, wird diese EMK dazu neigen, sich zu manifestieren. Ein Kurzschluss führt jedoch nicht dazu, dass sich eine EMK über ihn hinweg entwickelt, da er definitionsgemäß null Widerstand aufweist. Keine EMK kann sich mit dem Strom verbinden, um Energie zu bilden, daher bleibt die Energie im Feld. Jeder Versuch, Kräfte kollabieren zu lassen, verstärkt Ströme, die ihn gleich wieder nach außen drängen. Dies ist eine Form der Speicherung von Energie.

Sofortige Freisetzung von Energie als Unendlichkeit

Sehr interessante (und gefährliche) Phänomene manifestieren sich, wenn der Strompfad unterbrochen wird, wodurch unendlicher Widerstand erscheint. In diesem Fall ist der Widerstand am besten darzustellen durch seine Umkehrung, der Leitfähigkeit. Der Leitfähigkeit ist dann null. Da der Strom sofort verschwand, kollabiert das Feld mit einer Geschwindigkeit, die die des Lichtes erreicht. Da EMK direkt von der Fließgeschwindigkeit abhängt, tendiert sie gegen unendlich. Sehr starke Effekte werden erzeugt, weil das Feld versucht, Strom aufrechtzuerhalten, indem es die EMK erzeugt, die es benötigt. Wenn eine erhebliche Menge an Energie existiert, sagen wir mehrere Kilowattstunden (250 KWh für Blitzschlag), kann die daraus folgende Entladung tiefgreifendste Auswirkungen haben und völlig unzureichend geschützte Geräte zerstören.

Eine andere Form an Energie erscheint

Durch die schnelle Entladung der Induktivität erscheint ein neues Kraftfeld, dass die Rate an induktiver EMK-Formierung reduziert. Auch dieses Feld wird auch durch Feldlinien dargestellt, aber diese sind anderer Natur als diejenigen des Magnetismus. Diese Kraftlinien sind nicht eine Stromfluss-Ausprägung, sondern eine Elektro-Kompression oder Anspannung. Diese Anspannung wird als Stromspannung oder Potentialdifferenz bezeichnet.

Dielektrischer Energiespeicher räumlich anders als magnetischer Energiespeicher

Im Gegensatz zum Magnetismus wird die Energie nach innen forciert oder komprimiert anstatt nach außen. Dielektrische Kraftlinien drängen nach innen in den inneren Raum und entlang der Achse, anstatt wie in dem Magnetfeld nach außen zur Seite zu drücken. Da die Linien sich gegenseitig abstoßen, kann man gewisse Mengen an Breitseiten- oder Querbewegungen erwarten, aber das Phänomen ist grundsätzlich längs, longitudinal. Daraus ergibt sich ein interessantes Paradoxon, das bei der Kapazität bemerkt wird. Dies ist, je kleiner der durch die leitende Struktur umgrenzte Raum ist, desto mehr Energie kann gespeichert werden. Das ist das genaue Gegenstück zum Magnetismus. Beim Magnetismus können die Einheiten der Energiemengen als parallel arbeitend gedacht werden, aber die Einheiten der Energiemengen in Verbindung mit Dielektrizität können als in Reihe arbeitend gedacht werden.

Stromspannung verhält sich zu Dielektrizität wie Stromstärke zu Magnetismus

Bei Induktivität ist die Reaktion auf die Feldveränderung die Produktion von Stromspannung. Die Stromstärke ist nur proportional zur Stärke des Feldes und nicht zur Geschwindigkeit des Feldes. Bei der Kapazität wird das Feld nicht durch Stromstärke erzeugt, sondern durch Stromspannung. Diese Stromspannung muss einhergehen mit Stromstärke, um als Kraft zu existieren. Die Reaktion der Kapazität auf die Änderung der aufgebrachten Kraft ist die Erzeugung der Stromstärke. Die Stromstärke ist direkt proportional zur Geschwindigkeit der Feldstärke. Wenn sich die Stromspannung erhöht, eine Reaktion fließt der Strom in die Kapazität und damit die Energie sammelt. Wenn die Stromspannung ansteigt, fließt ein Reaktionsstrom in die Kapazität und dadurch sammelt sich Energie an. Wenn sich die Stromspannung nicht ändert, fließt kein Strom und die Kapazität speichert die Energie, die das Feld erzeugt hat. Sobald die Stromspannung abgezogen wird, wird die Kompression innerhalb des begrenzten Raumes befreit. Wenn die Energie vollständig zerstreut ist, verschwinden die Kraftlinien.

Noch einmal: die Grenzen von Null und Unendlichkeit

Weil die Stromversorgung, welche die Ladespannung bereitstellt, eine interne Leitfähigkeit aufweist, zieht – nach Abschalten der Stromversorgung – der Strom, der durch Leitfähigkeit ausläuft, die dielektrische Energie ab und wandelt sie in Wärme um. Wir werden eine perfekte Kapazität ohne Leitfähigkeitsverlust annehmen. Wenn wir die Spannungsversorgung vollständig abtrennen, indem wir die Anschlussenden des Kondensators öffnen, besteht per Definition kein Pfad für den Stromfluss eines offenen Schaltkreises. Wenn das Feld dazu neigt, sich auszudehnen, tendiert es zur Stromproduktion. Ein offener Stromkreis lässt jedoch keinen Stromfluss zu, da er keine Leitfähigkeit aufweist. Dann wird jeder Versuch hin zu einer Expansion des Feldes die Stromspannung erhöhen, die das Feld wieder zurück nach innen drängt. Daher wird Energie im Feld gespeichert bleiben. Diese Energie kann jederzeit zur Verwendung abgezogen werden. Dies ist eine weitere Form der Energiespeicherung.

Sofortige Energiefreisetzung ins Unendliche

Phänomene enormen Ausmaßes zeigen sich, wenn die Kriterien für Stromspannung oder Potentialdifferenz sofort unterbrochen werden, wie bei einem Kurzschluss. Der Effekt ist analog zu dem offenen Stromkreis des induktiven Stromes. Da die treibende Stromspannung sofort entzogen wird, explodiert das Feld gegen die begrenzenden Leiter mit einer Geschwindigkeit, die Licht überschreiten kann. Da der Strom direkt mit der Geschwindigkeit des Feldes in Beziehung steht, macht er einen Sprung ins Unendliche in seinem Versuch, eine endliche Stromspannung zu erzeugen über Null Widerstand hinweg. Wenn sich im dielektrischen Kraftfeld eine beträchtliche Energie befunden hätte, sagen wir einmal mehrere KWh, so hat die sich ergebende Explosion fast unfassbare Gewalt und kann einen Leiter beträchtlicher Dicke sofort verdampfen. Dielektrische Entladungen von großer Geschwindigkeit und Energie sind eines der unangenehmsten Erlebnisse, denen der Elektrotechniker in der Praxis begegnet.

Energie kehrt zur magnetischen Form zurück

Die starken Ströme, die durch die plötzliche Ausdehnung eines dielektrischen Feldes erzeugt werden, führen natürlich zu magnetischer Energie. Die Trägheit des Magnetfeldes begrenzt den Anstieg des Stroms auf einen realistischen Wert. Die Kapazität entleert ihre gesamte Energie in das Magnetfeld zurück und der gesamte Prozess beginnt von vorne. Die Umkehrung des Produkts aus magnetischer Speicherkapazität und dielektrischer Speicherkapazität repräsentiert die Frequenz oder Tonhöhe, bei der dieser Energieaustausch erscheint. Diese Tonhöhe kann Obertöne enthalten oder auch nicht, abhängig vom Ausmaß der Stromleiter, die die Energien begrenzen.

Charakteristische Impedanz als Darstellung der Pulsation des Energiefeldes

Das Verhältnis der magnetischen Speicherfähigkeit zu der des Dielektrikums wird als charakteristische Impedanz [ Scheinwiderstand ] bezeichnet. Dies ergibt das Verhältnis von maximaler Spannung zu maximalem Strom in der Oszillationsstruktur. Da der magnetische Energiespeicher jedoch nach außen gerichtet ist und der dielektrische Speicher nach innen gerichtet ist, pulsiert das gesamte oder doppelte Energiefeld in Form oder Größe. Die Achse dieser Pulsationskraft ist die Impedanz des Systems, die Oszillationen anzeigt, und Pulsation erscheint bei der Frequenz der Oszillation.

Energie in Materie

Sobald die Spannung oder Impedanz erhöht wird, liegt die Gewichtung auf dem nach innen gerichteten Fluss. Falls die Impedanz hoch ist und die Änderungsrate schnell genug ist (perfekte Obertonreihe), scheint es möglich, dass die Kompression der Energie sich in Materie transformieren würde und dass die Rückumwandlung dieser Materie in Energie sich mit dem Oszillationszyklus synchronisieren kann oder auch nicht. Dies kann als Superkapazität betrachtet werden, d.h. als stabile Langzeitumwandlung in Materie.

Missverständnisse der gegenwärtigen Theorie der Kapazität

Das Missverständnis, dass Kapazität das Ergebnis von sich ansammelnden Elektronen ist, hat unsere Sicht auf dielektrische Phänomene ernsthaft verzerrt. Auch die Theorie der Lichtgeschwindigkeit als Grenze des Energieflusses beschränkt unsere Fähigkeit, bestimmte Möglichkeiten in elektrischen Phänomenen zu visualisieren oder zu verstehen, während sie für magnetische Kraft und Materialgeschwindigkeit ausreichend ist. Die wahre Wirkungsweise der freien Raumkapazität kann am besten durch das folgende Beispiel veranschaulicht werden. Es wurde zuvor festgestellt, dass dielektrische Kraftlinien auf Stromleitern enden müssen. Keine Kraftlinie kann im Weltraum enden. Wenn wir irgendeinen Stromleiter nehmen und ihn zum entlegensten Teil des Universums entfernen, können sich keine Kraftlinien von dieser Elektrode zu anderen Stromleitern erstrecken. Er kann keine freie Speicherkapazität haben, unabhängig von der Größe der Elektrode, daher kann er keine Energie speichern. Dies deutet darauf hin, dass die freie Raumkapazität eines Objekts die Summe seiner gegenseitigen Kapazität zu allen leitenden Objekten des Universums ist.

Freie Rauminduktivität ist unendlich

Steinmetz weist in seinem Buch über das Allgemeine oder einheitliche Verhalten von Elektrizität, Theorie und Berechnung von Transienten Elektrischen Phänomenen und Schwingung, darauf hin, dass die Induktivität von jeder Einheitslänge, eines isolierten fadenförmigen Stromleiters unendlich sein muss. Da keine Bildströme existieren, die das Magnetfeld enthalten, kann es zu einer unendlichen Größe anwachsen. Diese große Menge an Energie kann nicht schnell zurückgeholt werden auf Grund der endlichen Ausbreitungsgeschwindigkeit des magnetischen Feldes. Dies ergibt eine nicht reaktive oder Energiekomponente für die Induktivität, die als elektromagnetische Strahlung bezeichnet wird.

Arbeiten Teslas, Steinmetz’ und Faradays

In der oben genannten Büchern von Steinmetz entwickelt er einige ziemlich eindeutige Gleichungen für die Kapazität [ Steinmetz 1909, S.11 ff ]. Tesla widmete einen großen Teil seiner Bemühungen dielektrischen Phänomenen und machte zahlreiche bemerkenswerte Entdeckungen auf diesem Gebiet. Ein Großteil dieser Arbeit muss noch vollständig entdeckt werden. Es ist meine Behauptung, dass die Phänomene der Dielektrizität weit offen sind für tiefgreifende Entdeckung. Es ist ironisch, dass wir das Konzept der Kraftlinien aufgegeben haben, das mit einem Phänomen verbunden ist – bemessen in der Einheit namens Farad nach Faraday – dessen Einsicht in Kräfte und Felder zu der Möglichkeit der Visualisierung der elektrischen Phänomene geführt hat.

Frage nach der Geschwindigkeit des dielektrischen Flusses

Es wurde festgestellt, dass alle magnetischen Kraftlinien auf sich selbst geschlossen sein müssen und dass alle dielektrischen Kraftlinien auf einer leitenden Oberfläche enden müssen. Aus diesen beiden Grundgesetzen lässt sich ableiten, dass keine Kraftlinie im freien Raum enden kann. Dies erzeugte eine interessante Frage hinsichtlich des Zustands der dielektrischen Flusslinien, bevor das Feld die Zeit hatte, sich zu dem neutralen Stromleiter auszubreiten. Während dieser Zeit würde es scheinen, dass die Kraftlinien, die den entfernten neutralen Stromleiter nicht erreicht hatten, an ihrer fortschreitenden Wellenfront im Weltraum enden würden. Man könnte daraus schließen, dass sich die Kraftlinien entweder sofort ausbreiten oder immer existieren und dass der modifizierte oder konjugierte [ gebeugte ] Raum innerhalb derselben Grenzen wie der gewöhnliche Raum existiert. Die Eigenschaften von Kraftlinien in diesem konjugierten Raum dürften nicht den Gesetzen des normal konzipierten Raumes gehorchen.

Quellenangaben

Faraday, M. 1855: Experimental Researches in Electricity. Bd. 3, Taylor and Francis, London, S. 1-587 (Facsimile Reprint; – https:/​/​archive.​org/​stream/​experimentalres01faragoog#page/​n5/​mode/​2up, abgerufen am 17. Juli 2018). (Übersetzung: Experimentelle Forschungen in Elektrizität)

Steinmetz, C. P. 1909: Theory and calculation of transient electric phenomena and oscillations. McGraw Publishing Company, New York, S. 1-556 ( https:/​/​archive.​org/​details/​theoryandcalcul12steigoog, abgerufen am 17. Juli 2018).

Steinmetz, C. P. 1911: Elementary lectures on electric discharges, waves and impulses, and other transients. McGraw-Hill Book Company, New York, S. 1-149 ( https:/​/​archive.​org/​details/​elementarylectur00steirich, abgerufen am 17. Juli 2018).

Thomson, J. J. 1904: Electricity and matter. In: Yale University Mrs. Hepsa Ely Silliman Memorial Lectures. Charles Scribner’s Sons, New York, S. 1-162 ( https:/​/​archive.​org/​details/​electricitymatte00thomiala, abgerufen am 17. Juli 2018).

Weiterführende Literatur

• Dollard, Eric. Theory of Wireless Power. [ Theorie drahtloser Energie ] BSRF, 1986. Druck. <#B0082>
• Dollard, Eric. Dielectric and Magnetic Discharges in Electrical Windings. [ Dielektrische und magnetische Entladungen in elektrischen Wicklungen ] BSRF, 1986. Druck. <#B0020>
• Dollard, Eric. Condensed Intro to Tesla Transformers. [ Komprimierte Einführung zu Tesla-Transformatoren. ] BSRF, 1986. Druck. <#B0018>
• Dollard, Eric. Symbolic Representation of the Generalized Electric Wave. [ Symbolische Darstellung der generalisierten elektrischen Welle ] BSRF, 1986. Druck. <#B0080>
• Dollard, Eric. Symbolic Representation of Alternating Electric Waves. [ Symbolische Darstellung alternierender elektrischer Wellen ] BSRF, 1986. Druck. <#B0079>