Einführung in die Dielektrizität & Kapazität (Eric P. Dollard)
Quelle: Artikel von Eric P. Dollard in The Journal of Borderland Research [Die Zeitschrift für Grenzbereich Forschung] (1990), Bd. 46, Nr. 02, siehe https://borderlandsciences.org/journal/vol/46/n02/Dollard_on_Dielectricity_Capacitance.html
Schlüsselwörter: Kapazität, Strom, Dielektrizität, elektrisches Feld, Faraday, Steinmetz, Tesla, Theorie, Stromspannung, Magnetismus, Energie, falsche Konzeption
Kapazität
Das Kapazitätsphänomen ist eine Art der elektrischen Energiespeicherung in der Form eines Feldes in einen umgrenzten Raum. Dieser Raum ist in der Regel beschränkt durch zwei parallele metallische Platten oder zweier metallischer Folien auf einem dazwischen liegenden Isolator oder Dielektrikum. Eine fast unendliche Vielzahl an komplexeren Strukturen kann Kapazität aufweisen, solange ein Unterschied im elektrischen Potential zwischen den verschiedenen Flächen der Struktur existiert. Die oszillierende Spule stellt eine Möglichkeit, als ein Kondensator komplexer Form, dar und diese wird hier präsentiert.
Kapazität unzureichend erklärt
Die Auffassung der Kapazität die heutzutage angewendet wird, ist vollkommen ungeeignet für das richtige Verständnis dieses Effekts. Steinmetz erwähnt dies in seinem einführenden Buch Elektrische Entladungen, Wellen und Impulse. Zitat [ S. 13 ], Unglücklicherweise, ist beim Umgang mit dielektrischen Feldern zum großen Teil noch die prähistorische Konzeption der elektrostatischen Ladung (Elektron) auf dem Stromleiter vorhanden, und durch deren Gebrauch zerstört es die Entsprechung zwischen den beiden Komponenten des elektrischen Feldes, der magnetischen und dielektrischen, und macht die Erwägung dielektrischer Felder unnötig kompliziert.
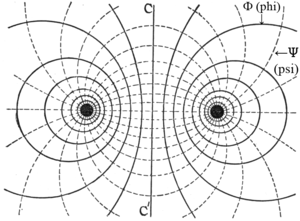
|
| Abb. 1a — Elektrisches Feld eines Stromkreises. [ Φ magnetischer Fluss; Ψ dielektrischer Fluss; aus Steinmetz (1911, S.11) ] |
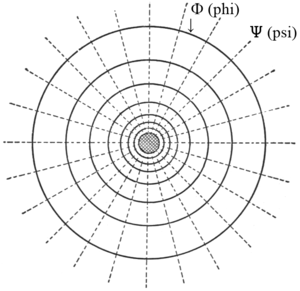
|
| Abb. 1b — Elektrisches Feld eines Stromleiters. [ Φ magnetischer Fluss; Ψ dielektrischer Fluss; aus Steinmetz (1911, S.11) ] |
Kraftlinien als Darstellung der Dielektrizität
Steinmetz führt weiter aus [ S. 14 ], Es ist offensichtlich nicht sinnvoller, wenn man den Kapazitätsstrom als Strom denkt, der den Leiter mit einer Menge Elektrizität auflädt, als wenn man von der Induktionsspannung spricht, die den Leiter mit einer Menge Magnetismus auflädt. Aber die letztgenannte Konzeption, zusammen mit der Vorstellung einer Menge an Magnetismus, etc., verschwand seit Faradays Darstellung des magnetischen Feldes mittels Kraftlinien.
Die Gesetze der Kraftlinien
Alle Linien der magnetischen Kraft sind in sich selbst geschlossen, alle dielektrischen Kraftlinien enden auf Stromleitern, aber können geschlossene Schleifen in elektromagnetischer Strahlung bilden. Diese stellen die grundlegenden Gesetze der Kraftlinien dar. Man kann anhand dieser Gesetze sehen, dass jede Kraftlinie nicht einfach im Raum enden kann.
Faraday & Kraftlinien-Theorie
Faraday war überzeugt, dass die Fernwirkung nicht durch leeren Raum möglich ist, oder mit anderen Worten [ S.293 in „Experimentelle Forschungen in der Elektrizität“ Bd.3 ], Materie kann nicht wirken, wo sie nicht ist.
Er erachtete Raum als von Linien der Kraft durchzogen. Fast jeder ist vertraut mit den Mustern, die durch Eisenspäne um einen Magneten geformt werden. Diese Späne wirken als zahlreiche kleine Kompasse und orientieren sich entlang der bestehenden Feldlinien rund um die Pole des Magneten. Experimentieren hat gezeigt, dass ein Magnetfeld eine faserige Konstruktion besitzt. Indem eine Drahtspule ein starkes Magnetfeld passiert und durch belauschen des Spulenausgangs mittels Kopfhörer, wird der Experimentator ein kratzendes Geräusch feststellen. J. J. Thompson führte weitere Experimente mit der Ionisation von Gasen durch, die zeigen, dass das Feld nicht kontinuierlich, sondern faserartig ist (ELEKTRIZITÄT UND MATERIE, 1904).
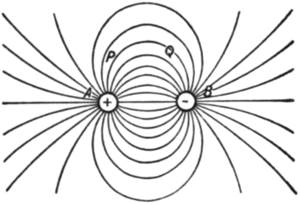
|
| Abb. 2 [ Elektrische Körper mit gleichwertigen, aber entgegengesetzten Ladungen; aus Thomson (1904, S.10) ] |
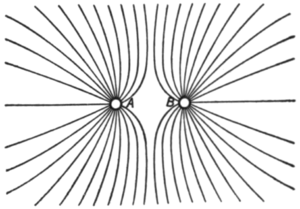
|
| Abb. 3 [ Elektrische Körper mit gleichen Ladungen; aus Thomson (1904, S.11) ] |
Physikalische Eigenschaften von Kraftlinien
Betrachte den Raum zwischen den Polen eines Magneten oder Kondensators als Fülle an Linien elektrischer Kraft. Siehe Abb. 1. Diese Kraftlinien wirken als eine Menge an gedehnten und sich gegenseitig abstoßend Federn. Jeder, der die Pole zweier Magneten zusammengedrückt hat, hat diese federnde Masse gefühlt. Beobachten wir Abb. 2. Beachte die dichteren Linien der Kraft entlang AB zwischen den Polen, und dass mehr Linien an A B zugewandt sind als nach außen in die Unendlichkeit hinausragen. Betrachte nun die Effekte der Kraftlinien an A. Diese Linien sind in einem Zustand der Spannung und ziehen an A. Weil mehr an A in Richtung B zurück ziehen, als diejenigen, die an A weg von B ziehen, haben wir die Phänomene der physikalischen Anziehung. Jetzt beobachten wir Abb. 3. Beachte nun, dass die Pole eher gleichartig sind statt ungleichartig, mehrere oder alle Linien ziehen A von B weg; die Phänomene der physikalischen Abstoßung.
Masse im Zusammenhang mit Kraftlinien in Bewegung
Die Kraftlinie kann man klarer verstehen, wenn man sie als ein Krafttubus oder einen langen, dünnen Zylinder abbildet. Maxwell stellte die Idee vor, die Gespanntheit eines Krafttubus ist repräsentativ für die elektrische Kraft (Volt/Zoll), und zusätzlich zu dieser Gespanntheit, gibt es ein Medium, durch das diese Tubusse passieren. Es gibt einen hydrostatischen Druck gegen das Medium oder den Äther. Der Wert dieses Druckes ist die Hälfte des Produkts aus dielektrischer und magnetischer Dichte. Dann gibt es Druck im rechten Winkel zu einem elektrischen Krafttubus. Wenn durch das Anwachsen eines Feldes sich der Krafttubus seitwärts oder in der Weite ausbreitet, stellt das Ziehen der Breitseite durch das Medium die magnetische Reaktion auf das Wachstum in der Intensität des elektrischen Stroms dar. Jedoch, wenn ein Krafttubus dazu gebracht wird, sich zum Ende zu bewegen, wird er durch das Medium gleiten mit wenig oder gar keinem Ziehen, da wenig Angriffsfläche geboten wird. Dies erklärt möglicherweise, warum bei bestimmten Experimenten von Tesla kein Magnetfeld assoziiert ist, die Bewegung an Energie zum Gegenstand haben ohne begleitendes magnetisches Feld.
Inductance as an Analogy to Capacity
Much of the mystery surrounding the workings of capacity can be cleared by close examination of inductance and how it can give rise to dielectric phenomena. Inductance represents energy storage in space as a magnetic field. The lines of force orientate themselves in close loops surrounding the axis of current flow that has given rise to them. The large the space between this current and its images or reflections, the more energy that can be stored in the resulting field.
Mechanism of Storing Energy Magnetically
The process of pushing these lines or loops outward, causing them to stretch, represents storing energy as in rubber band. A given current strength will hold a loop of force at a given distance from conductor passing current hence no energy movement. If the flow of current increases, energy is absorbed by the field as the loops are then pushed outward at a corresponding velocity. Because energy is in motion an E.M.F. [ electro-motive force ] must accompany the current flow in order for it to represent power. The magnitude of this EMF exactly corresponds to the velocity of the field. Then if the current ceases changing in magnitude thereby becoming constant, no EMF accompanies it, as no power is being absorbed. However, if the current decreases and represents then a negative velocity of field as the loops contract. Because the EMF corresponds exactly to velocity it reverses polarity and thereby reverses power so it now moves out of the field and into the current. Since no power is required to maintain a field, only current, the static or stationary field, represents stored energy.
The Limits of Zero and Infinity
Many interesting features of inductance manifest themselves in the two limiting cases of trapping the energy or releasing it instantly. Since the power supply driving the current has resistance, when it is switched off the inductance drains its energy into this resistance that concerts it into the form of heat. We will assume a perfect inductor that has no self resistance. If we remove the current supply by shorting the terminals of the inductor we have isolated it without interrupting any current. Since the collapse of field produces EMF this EMF will tend to manifest. However, a short circuit will not allow an EMF to develop across it as it is zero resistance by definition. No EMF can combine with current to form power, therefore, the energy will remain in the field. Any attempt to collapse forces increased currents which pushes it right back out This is one form of storage of energy.
Instant Energy Release as Infinity
Very interesting (and dangerous) phenomena manifest themselves when the current path is interrupted, thereby causing infinite resistance to appear. In this case resistance is best represented by its inverse, conductance. The conductance is then zero. Because the current vanished instantly the field collapses at a velocity approaching that of light. As EMF is directly related to velocity of flux, i tends towards infinity. Very powerful effects are produced because the field is attempting to maintain current by producing whatever EMF required. If a considerable amount of energy exists, say several kilowatt hours[1] (250 KWH for lightning stroke), the ensuing discharge can produce most profound effects and can completely destroy inadequately protected apparatus.
- ↑ The energy utilized by an average household in the course of one day.
Another Form of Energy Appears
Through the rapid discharge of inductance a new force field appears that reduces the rate of inductive EMF formation. This field is also represented by lines of force but these are of a different nature than those of magnetism. These lines of force are not a manifestation of current flow but of an electric compression or tension. This tension is termed voltage or potential difference.
Dielectric Energy Storage Spatially Different than Magnetic Energy Storage
Unlike magnetism the energy is forced or compressed inwards rather than outwards. Dielectric lines of force push inward into internal space and along axis, rather than pushed outward broadside to axis as in the magnetic field. Because the lines are mutually repellent certain amounts of broadside or transverse motion can be expected but the phenomena is basically longitudinal. This gives rise to an interesting paradox that will be noticed with capacity. This is that the smaller the space bounded by the conducting structure the more energy that can be stored. This is the exact opposite of magnetism. With magnetism, the units volumes of energy can be though of as working in parallel but the unit volumes of energy in association with dielectricity can be thought of as working in series.
Voltage is to Dielectricity as Current is to Magnetism
With inductance the reaction to change of field is the production of voltage. The current is proportionate to the field strength only and not velocity of field. With capacity the field is produced not by current but voltage. This voltage must be accompanied by current in order for power to exist. The reaction of capacitance to change of applied force is the production of current. The current is directly proportional to the velocity of field strength. When voltage increases a reaction current flows into capacitance and thereby energy accumulates. If voltage does not change no current flows and the capacitance stores the energy which produced the field. If the voltage decreases then the reaction current reverses and energy flows out of the dielectric field.As the voltage is withdrawn the compression within the bounded space is relieved. When the energy is fully dissipated the lines of force vanish.
Again the Limits of Zero and Infinity
Because the power supply which provided charging voltage has internal conductance, after it is switched off the current leaking through conductance drains the dielectric energy and converts it to heat. We will assume a perfect capacitance having no leak conductance. If we completely disconnect the voltage supply by open circuiting the terminals of the capacitor, no path for current flow exists by definition of an open circuit. If the field tends to expand it will tend towards the production of current. However, an open circuit will not allow the flow of current as it has zero conductance. Then any attempt towards field expansion raises the voltage which pushes the field back inwards. Therefore, energy will remain stored in the field. This energy can be drawn for use at any time. This is another form of energy storage.
Instant Energy Release as Infinity
Phenomena of enormous magnitude manifest themselves when the criteria for voltage or potential difference is instantly disrupted, as with a short circuit. The effect is analogous with the open circuit of inductive current. Because the forcing voltage is instantly withdrawn the field explodes against the bounding conductors with a velocity that may exceed light. Because the current is directly related to the velocity of field it jumps to infinity in its attempt to produce finite voltage across zero resistance. If considerable energy had resided in the dielectric force field, again let us say several KWH the resulting explosion has almost inconceivable violence and can vaporize a conductor of substantial thickness instantly. Dielectric discharges of great speed and energy represent one of the most unpleasant experiences the electrical engineer encounters in practice.
Energy Returns to Magnetic Form
The powerful currents produced by the sudden expansion of a dielectric field naturally give rise to magnetic energy. The inertia of the magnetic field limits the rise of current to a realistic value. The capacitance dumps all its energy back into the magnetic field and the whole process starts over again. The inverse of the product of magnetic storage capacity and dielectric storage capacity represents the frequency or pitch at which this energy interchange occurs. This pitch may or may not contain overtones depending on the extent of conductors bounding the energies.
Characteristic Impedance as Representation of Pulsation of Energy Field
The ratio of magnetic storage ability to that of the dielectric is called the characteristic impedance. This gives the ratio of maximum voltage to maximum current in the oscillatory structure. However, as the magnetic energy storage is outward and the dielectric storage is inward the total or double energy field pulsates in shape or size.The axis of this pulsation of force is the impedance of the system displaying oscillations and pulsation occurs at the frequency of oscillation.
Energy into Matter
As the voltage or impedance is increased the emphasis is on the inward flux. If the impedance is high and rate of change is fast enough (perfect overtone series), it would seem possible the compression of the energy would transform it into matter and the reconversion of this matter into energy may or may not synchronize with the cycle of oscillation. This is what may be considered supercapacitance, that is, stable long term conversion into matter.
Misconceptions of Present Theory of Capacitance
The misconception that capacitance is the result of accumulating electrons has seriously distorted our view of dielectric phenomena. Also the theory of the velocity of light as a limit of energy flow, while adequate for magnetic force and material velocity, limits our ability to visualize or understand certain possibilities in electric phenomena. The true workings of free space capacitance can be best illustrated by the following example. It has been previously stated that dielectric lines of force must terminate on conductors. No line of force can end in space. If we take any conductor and remove it to the most remote portion of the universe, no lines of force can extend from this electrode to other conductors. It can have no free space capacity, regardless of the size of the electrode, therefore it can store no energy. This indicates that the free space capacitance of an object is the sum mutual capacity of it to all the conducting objects of the universe.
Free Space Inductance is Infinite
Steinmetz in his book on the general or unified behavior of electricity The Theory and Calculation of Transient Electric Phenomena and Oscillation, points out that the inductance of any unit length of an isolated filamentary conductor must be infinite. Because no image currents exist to contain the magnetic field it can grow to infinite size. This large quantity of energy cannot be quickly retrieved due to the finite velocity of propagation of the magnetic field. This gives a non reactive or energy component to the inductance which is called electromagnetic radiation.
Work of Tesla, Steinmetz, and Faraday
In the aforementioned books of Steinmetz he develops some rather unique equations for capacity [ Steinmetz 1909, p.11 ff. ]. Tesla devoted an enormous portion of his efforts to dielectric phenomena and made numerous remarkable discoveries in this area. Much of this work is yet to be fully uncovered. It is my contention that the phenomena of dielectricity is wide open for profound discovery. It is ironic that we have abandoned the lines of force concept associated with a phenomena measure in the units called farads after Faraday, whose insight into forces and fields has led to the possibility of visualization of the electrical phenomena.
Question as to the Velocity of Dielectric Flux
It has been stated that all magnetic lines of force must be closed upon themselves, and that all dielectric lines of force must terminate upon a conducting surface. It can be inferred from these two basic laws that no line of force can terminate in free space. This created an interesting question as to the state of dielectric flux lines before the field has had time to propagate to the neutral conductor. During this time it would seem that the lines of force, not having reached the distant neutral conductor would end in space at their advancing wave front. It could be concluded that either the lines of force propagate instantly or always exists and are modified or conjugate space exists within the same boundaries as ordinary space. The properties of lines of force within this conjugate space may not obey the laws of normally conceived space.
References
Further Reading
- Dollard, Eric. Theory of Wireless Power. BSRF, 1986. Print. <#B0082>
- Dollard, Eric. Dielectric and Magnetic Discharges in Electrical Windings. BSRF, 1986. Print. <#B0020>
- Dollard, Eric. Condensed Intro to Tesla Transformers. BSRF, 1986. Print. <#B0018>
- Dollard, Eric. Symbolic Representation of the Generalized Electric Wave. BSRF, 1986. Print. <#B0080>
- Dollard, Eric. Symbolic Representation of Alternating Electric Waves. BSRF, 1986. Print. <#B0079>